Le Beta ou la mesure du risque d’un actif

Le Bêta est un outil de mesure du risque d’un actif notamment utilisé dans le modèle d’évaluation du CAPM. On l’utilisera entre autres pour mettre en place des stratégies de limitation des risques.

CAPM : Le “Capital Asset Pricing Model” (CAPM) ou Modèle d’évaluation des actifs financiers (MEDAF) est le modèle d’évaluation le plus célèbre et le plus utilisé malgré le fait que sa pertinence empirique soit très discutée.

Créé par Sharpe, Lintner et Mossin dans les années 60 et basé sur des études réalisées par Markowitz en 1952 (la théorie moderne du portefeuille), cet outil décrit la relation entre le risque d’un actif financier et la rentabilité espérée de cet actif.

L’idée générale sur laquelle le modèle CAPM est basée est la suivante : les investisseurs sont rémunérés par la valeur temps de l’argent et par le risque. La valeur temps de l’argent est représentée par le taux sans risque, qui correspond généralement au taux de placement le plus faible mais le moins risqué, type livret A.

Le risque est représenté par le Beta, rapport historique entre la volatilité de l’actif et celle du marché.

Voici la formule de base du modèle :

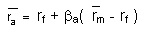
avec :
: rentabilité espérée de l’actif financier
 : taux sans risque
: Beta de l’actif financier
: rentabilité espérée du marché

Ainsi le CAPM décrit la rentabilité de l’actif comme la rentabilité de l’actif sans risque additionnée à une prime de risque marché (rentabilité du marché moins rentabilité de l’actif sans risque) pondérée par le beta de l’actif.

Voyons comment calculer les composants de la formule :

: comme dit précédemment, le taux sans risque représente le taux de placement le plus faible mais le moins risqué type “livret A”. Nul besoin de le calculer donc.

: la rentabilité espérée du marché : on prend la rentabilité historique du marché de référence (par exemple l’indice correspondant à la valeur) sur une certaine période (2 ans, 5 ans, 10 ans…).

 : Le Beta de l’actif financier se définit comme le rapport de la covariance de la rentabilité de l’actif avec celle du marché à la variance de la rentabilité du marché.

on a ainsi la formule suivante : Beta = Covariance (R.actif, R.marché) / Variance (R.marché).

La manière la plus simple de calculer un Beta est la méthode historique. Ainsi, “R.actif” sera la rentabilité historique de l’actif, de même que “R.marché” sera la rentabilité historique du marché.

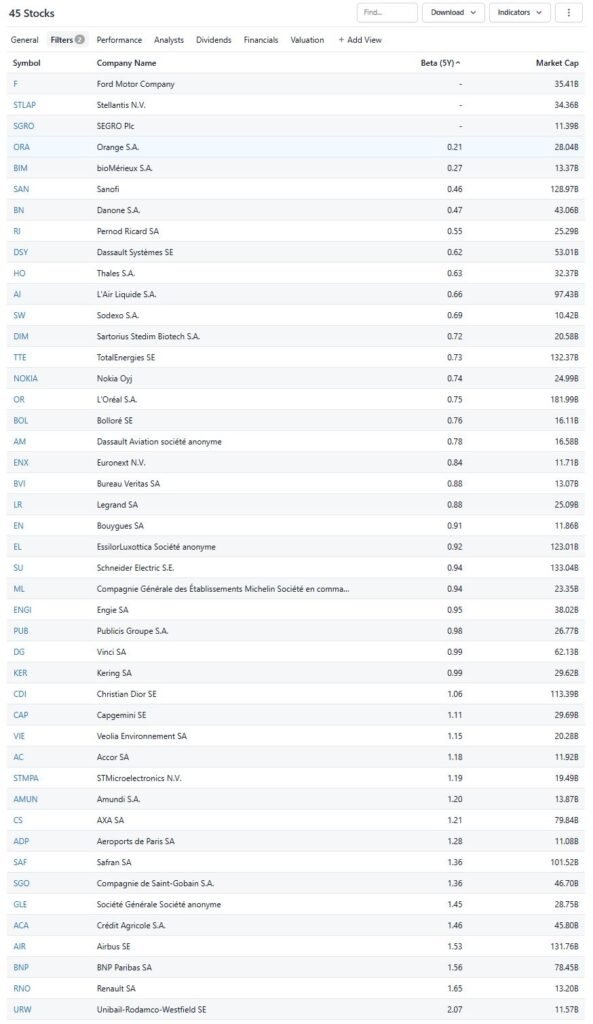
De manière pratique, plus le Beta sera proche de 1, plus les variations du marché seront suivies de manière équivalente par l’actif.

Pour déterminer si un actif offre une opportunité d’investissement, il faudra comparer l’espérance de rendement calculée avec le CAPM au rendement prévu sur la valeur, calculé par exemple de manière fondamentale à partir du PER ou autres techniques d’évaluations. On peut ainsi déterminer si le prix actuel de l’actif est à un niveau bas ou élevé.

L’univers du CAPM doit obéir à certaines règles bien précises pour que la formule de la rentabilité de l’actif fonctionne. Voici les différentes hypothèses de bases, tirées principalement des travaux de Markowitz sur la théorie moderne du portefeuille :

– il n’y a pas de coûts de transactions ou de taxes
– la vente à découvert ou l’achat d’un titre n’a aucune incidence sur son prix
– les investisseurs sont averses au risque et rationnels
– tous les investisseurs ont le même horizon d’investissement
– les investisseurs contrôlent le risque de leur portefeuille par la diversification
– le marché est entièrement libre et tous les actifs peuvent y être échangés.
– les investisseurs peuvent emprunter et prêter des montants illimités au taux sans risque
– toutes les informations sur le marché sont disponibles pour tous les investisseurs
– la concurrence sur les marchés et parfaite et non faussée
– tous les actifs financiers peuvent être divisés en actifs de plus petite taille

Vous l’aurez compris, l’univers du CAPM est parfait et ne peut consister qu’en une approximation grossière du monde réel. C’est pourquoi le modèle du CAPM est tant controversé et a fait l’objet d’attaques virulentes de la part de nombreux théoriciens de la finance.

Voici certaines anomalies relevées au fil du temps après des résultats empiriques concernant le modèle du CAPM :

– il est impossible de calculer avec exactitude la rentabilité espérée du marché, ce qui fausse le résultat final.

– L’effet taille ou PER n’est pas pris en compte dans le modèle. En effet, il a été mis en évidence que les titres à faible capitalisation et/ou à faible PER avaient des rentabilités supérieures aux titres à forte capitalisation et/ou PER élevé.

De nombreuses autres critiques ont été émises à l’encontre du CAPM. Malgré cela, ce modèle demeure un grand classique et reste l’une des théories les plus utilisés dans la finance moderne.

Le principe de cet outil est de comparer les mouvements effectués par un actif par rapport à son marché de référence, ce qui permet de déterminer son niveau de risque par rapport aux autres actifs de référence. La mesure est effectuée en comparant la rentabilité de l’actif à celle du marché. On peut aussi réduire le marché à un indice boursier (CAC 40, Dow Jones, etc.)

Mathématiquement, le Bêta de l’actif financier se définit comme le rapport de la covariance de la rentabilité de l’actif avec celle du marché à la variance de la rentabilité du marché.

Comment calculer le Bêta ?

La manière la plus simple de calculer un Bêta est la méthode historique. On comparera donc les données de rentabilité historique de l’actif à celles du marché.

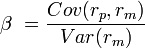
avec rp : rentabilité de l’actif et rm : rentabilité du marché

Exemple

Concrètement, prenons l’exemple d’une action du CAC 40 qui possède un Bêta de 1,8. Cela signifie que si l’indice CAC 40 varie de 10%, l’action devrait théoriquement varier de 18%, elle amplifiera donc les mouvements du marché puisque son Bêta est supérieur à 1.

A l’inverse, si une action a un Bêta de 0,7, elle variera moins violemment que son marché de référence : si le CAC 40 varie de 10%, elle devrait effectuer un mouvement de 7% seulement.

On peut aussi rencontrer d’autres situations. Par exemple un coefficient Bêta négatif signifiera que l’action évolue en sens inverse de son marché. Si le Bêta est égal à 0, cela indique que l’actif et son marché ne sont pas du tout corrélés, leurs variations sont totalement indépendantes.

Utilisation du Beta

Le Bêta permettra de se faire une idée du comportement d’un titre vis à vis de son indice pour mettre en place un portefeuille diversifié. Toutefois attention, le calcul du coefficient est valable à un instant donné, il évolue dans le temps et un Bêta peut devenir négatif quelques mois plus tard.

Au delà de ce calcul du rapport historique de la volatilité du prix d’un actif financier et de son marché en général (ou son indice), le Bêta est utilisé dans d’autres modèles.